Réglettes Cuisenaire sont un simple, mais ingénieux, outil pour l'enseignement des relations mathématiques à de jeunes enfants. Plus souvent utilisé en Europe qu'aux États-Unis, ils ont d'abord été développés par le professeur belge Georges Cuisenaire dans les années 1940. Les blocs rectangulaires en bois viennent dans 10 couleurs différentes et 10 longueurs différentes. Les manipuler aide les élèves à visualiser ce qui serait autrement des concepts mathématiques abstraits et peuvent les conduire à une meilleure compréhension des calculs utilisés dans l'arithmétique, la mesure et de la géométrie.
 (Karen Amundson / Demand Media)
(Karen Amundson / Demand Media)Étape 1:Laissez le libre-jeu d'enfant avec un ensemble de tiges se habituer à eux et aussi pour explorer ses propres idées à leur sujet.
 Karen Amundson / Demand Media
Karen Amundson / Demand Media Étape 2:Demandez-lui de jeter les tiges à côté de l'autre sur une table dans l'ordre de la taille, de la plus petite tige blanche jusqu'à la tige d'orange plus longue. Elle trouvera qu'ils forment une "escalier."
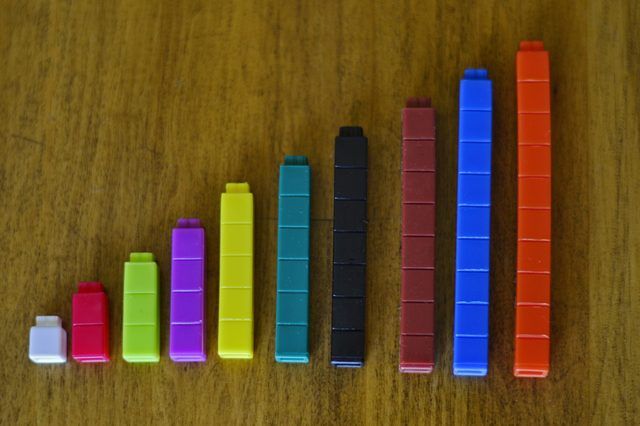 Karen Amundson / Demand Media
Karen Amundson / Demand Media Etape 3:Attribuer les tiges d'une valeur numérique à partir du numéro 1 pour la plus petite au numéro 10 pour le plus grand. Demander aux élèves de pointer vers les tiges comme elle répète les valeurs de chaque.
 Karen Amundson / Demand Media
Karen Amundson / Demand Media Étape 4:Placez la tige numéro 3 séparément du reste et de demander à l'élève d'exposer deux autres tiges qui, mises bout à bout sera la même longueur que le nombre 3. Elle se trouve que les numéros 1 et 2 placés en bout fin - dans un "train," d'utiliser une terminologie Cuisenaire - va correspondre exactement à la longueur du numéro 3. Utilisez cette illustration pour parler plus.
 Karen Amundson / Demand Media
Karen Amundson / Demand Media Etape 5:Continuer à utiliser différentes longueurs des tiges pour illustrer plus en demandant aux étudiants de former des trains de différentes longueurs et les faire correspondre.
 Karen Amundson / Demand Media
Karen Amundson / Demand Media Etape 6:Illustrer la soustraction de la même manière, en formant des trains, puis enlever les tiges de différentes valeurs.
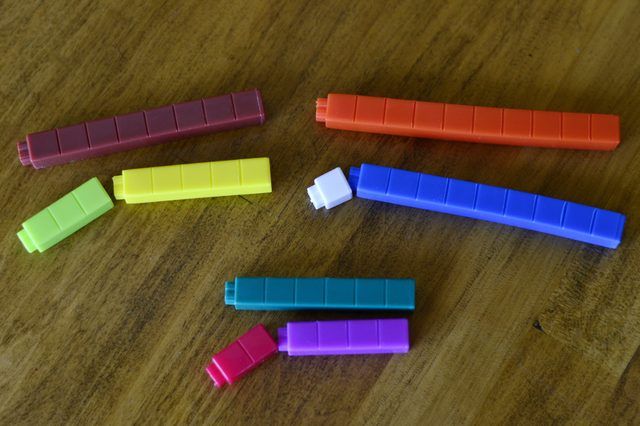 Karen Amundson / Demand Media
Karen Amundson / Demand Media Etape 7:Passer à la multiplication et la division, en utilisant plusieurs ensembles de tiges, et de nouveau en utilisant les trains. Par exemple, cinq blancs numéro 1 tiges égale à la longueur d'un jaune numéro 5 tige, démontrant que 5 fois 1 est de 5.
 Karen Amundson / Demand Media
Karen Amundson / Demand Media Étape 1:Demander aux élèves d'utiliser le blanc numéro 1 tige, qui est de 1 centimètre de long, pour mesurer les autres tiges, et d'exprimer leurs longueurs en centimètres.
 Karen Amundson / Demand Media
Karen Amundson / Demand Media Étape 2:Demander à l'élève d'utiliser les ensembles de tiges pour mesurer un objet dans la salle de classe, tels que la longueur d'un bureau. L'étudiant peut trouver, il peut utiliser le numéro 10 tige d'orange 10 centimètres de long pour la plupart de la longueur, mais doivent utiliser les plus petites tiges pour finir.
 Karen Amundson / Demand Media
Karen Amundson / Demand Media Etape 3:Commencer à travailler avec les régions. Demander aux élèves de construire une forme bidimensionnelle sur le bureau en utilisant une variété de tiges, et en comptant les valeurs, l'aider à calculer la zone couverte par sa forme. Commencez avec des carrés simples constitués d'une seule couleur, et de passer ensuite à des formes plus complexes.
 Karen Amundson / Demand Media
Karen Amundson / Demand Media Étape 4:Introduire le concept du volume en affectant la valeur de 1 unité cube blanc numéro 1 tige.
 Karen Amundson / Demand Media
Karen Amundson / Demand Media Etape 5:Laissez les étudiants utilisent de multiples numéro 1 tiges pour construire des figures cubes en trois dimensions des volumes variables, et de les exprimer les volumes de leurs chiffres en unités cubes.
 Karen Amundson / Demand Media
Karen Amundson / Demand Media